50-річну математичну "проблему з диваном" нарешті вдалось вирішити

Ймовірно, математики не будуть тими, до кого ви звертатиметеся у день переїзду. Очевидно: навіщо вам знадобиться математик в таких умовах? Але саме математикам вдалось вирішити 50-річну "проблему з диваном".

• Вчені розгадали правила цієї чудернацької настільної гри, які було втрачено 4000 років

Деталі

Джінеон Бек, ентузіаст комбінаторики та геометрії з Університету Йонсей у Кореї щойно опублікував 100-сторінкове вирішення цієї проблеми, щоб ми всі могли придбати ідеальний диван, з яким не застрягнемо на сходовій клітці.

У 1966 році австрійсько-канадський математик Лео Мозер формалізував проблему, яка мучила людство з того часу, як з'явилися дивани та повороти. Звучить задача просто: який найбільший двовимірний об’єкт може успішно обійти L-подібний кут?

Для коридору шириною в одну одиницю, стілець в одну квадратну одиницю пройде без проблем. З іншого боку, об'єкт у дві квадратні одиниці ніколи не пролізе. Але якщо форма гіпотетичного дивану не буде прямокутною?

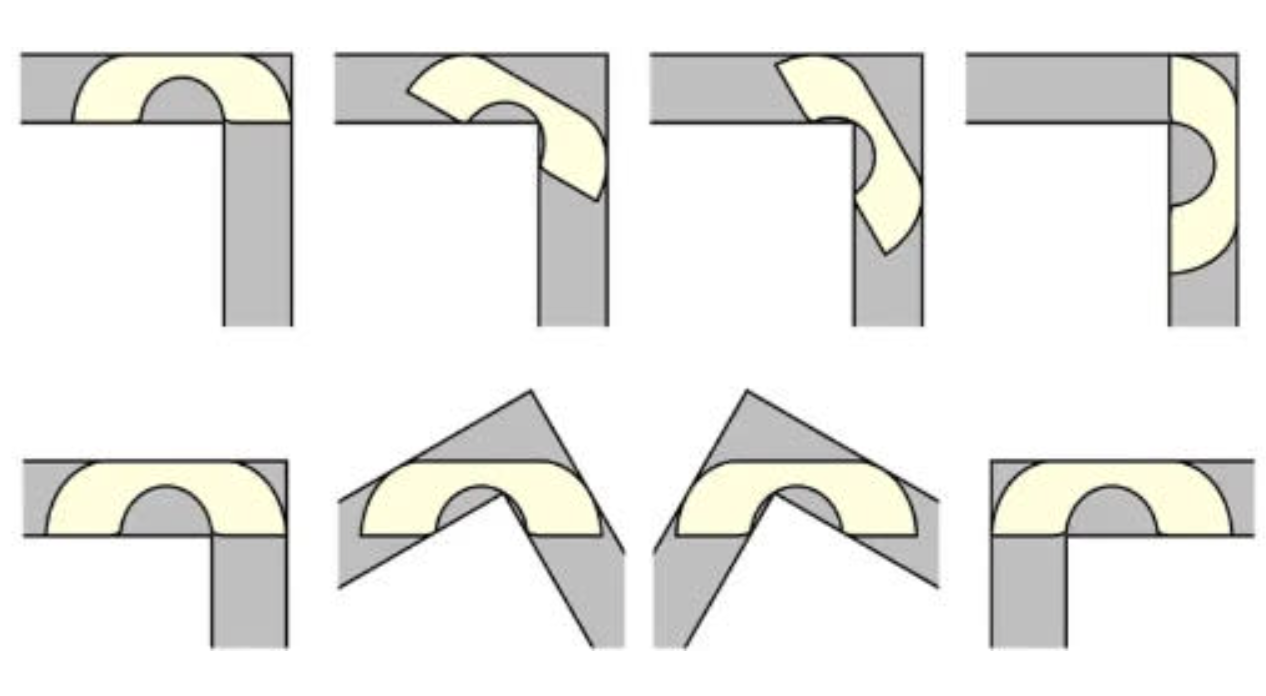
Всього через два роки після того, як Мозер сформулював задачу, британський математик Джон Хаммерслі виявив, що площа дивана, що складається з розсіченого півкола, розділеного квадратом із вилученим півколом, може мати площу 2,2074 одиниці, і все одно пролізти через L-подібний поворот шириною в одну одиницю. Хаммерслі також встановив верхню межу для дизайну – ніщо більш як 2,8284 одиниці не могло пролізти. Тобто найбільший можливий розмір дивана має бути десь між значеннями 2,2074 та 2,8284 одиниці.

Минуло майже чверть століття, перш ніж вчений Рутгерського університету на ім’я Джозеф Гарвер запропонував дещо змінити дизайн дивана Хаммерслі, округливши кілька країв додатковими дугами та знайшовши форму, яка додає дроби до попередньої нижньої межі, щоб підняти мінімальну межу до понад 2,2195 одиниці. Але точне максимальне число досі було невідомо.

У 2018 році математик з Інституту Санта-Фе Йоав Каллус і Ден Ромік з Каліфорнійського університету в Девісі використали комп’ютерну схему, щоб показати, що розмір дивана може досягати максимум 2,37 одиниці. Тобто найбільша можлива форма тепер десь між 2,2195 та 2,37 одиниці.

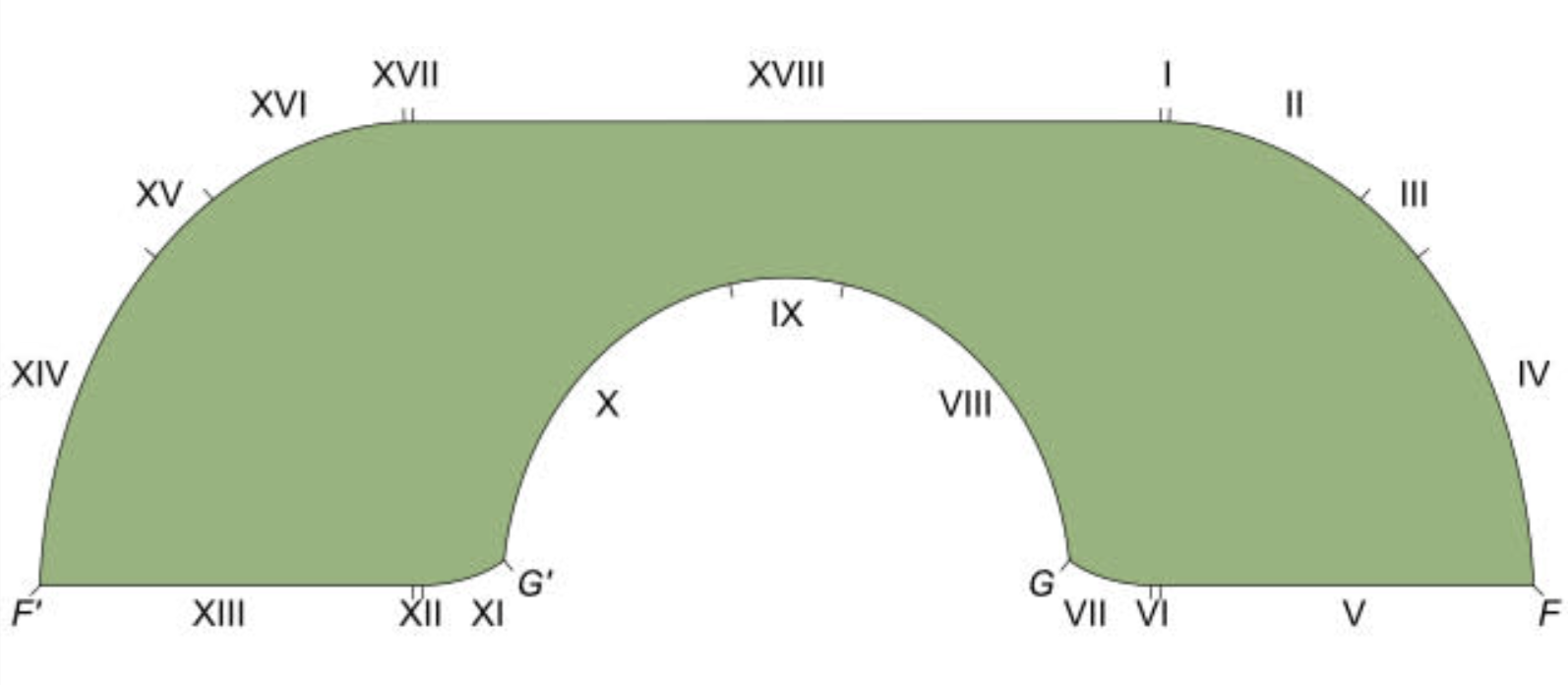
Для останнього доказу Джінеон Бек застосував трохи математичного чаклунства, відомого як ін’єктивна функція, щоб відобразити вдалі форми дивана Гарвера, зафіксувавши ключові властивості перед розширенням їх у все більших розмірах, щоб раз і назавжди довести, наскільки великим може бути диван, схожий на той, який пропонував Гарвер.

Виявилось, що ​​2,2195 одиниці – це кращий диван для коридору шириною в 1 одиницю та L-подібного кута, як запропонував Гарвер у 1992 році. Тобто знадобилося 32 роки, щоб довести що Гарвер запропонував ідеальну форму для найбільшого дивана, який може пройти через прямий кут.

Раніше ми повідомляли, що у США старшокласниці запропонували "неможливе" доведення 2000-річного математичного правила.